공부/선형대수
선형 대수 - 2. 행렬, 간단한 행 연산
하나리나
2023. 9. 3. 22:52
반응형
아래와 같이 세 개의 방정식이 있습니다.
더보기
3x - 2y + z = 2
-x - 5y + 4z = 1
x + 4y - 6z = -9
위 방정식을 아래와 같은 시스템 (혹은 행렬)으로 나타낼 수 있습니다.

블로그에서 완벽하게 다루진 않았지만,
3개의 방정식을 Ax = B 형태로 나타낼 수 있고, 이 시스템에서 A와 B를 이용하여 행렬로 표기하는 것입니다.
다시 완전한 행렬로 나타내면 아래와 같습니다.
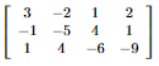
이제 이 행렬에서 몇 가지 가능한 행 연산을 알아보도록 하겠습니다.
(1) 행 치환 (switching rows)
만약, 1행과 2행을 치환한다면 (R1 ↔ R2), 아래와 같이 행렬을 구성할 수 있겠습니다. 단지 1행과 2행의 순서만 바뀐 것입니다.

(2) 스칼라배 (Scaling)
이제 2행에 3을 곱해 보겠습니다. (3R1 →R1). 즉, Row1에 3을 곱해서 Row1을 대체하는 것입니다.

(3) 행끼리 더하기 (Adding) - 뺄셈도 가능
1행과 2행을 더해보겠습니다. (R1+R2 → R2), R1과 R2 더한 것을 R2에 적는 것입니다.
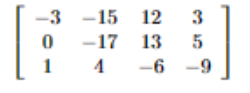
다음 시간에는 행렬로 연립방정식을 본격적으로 풀어보려고 합니다. 이번 시간에 배운 세 가지 방법인 행 치환, 스칼라배, 행끼리 더하기(빼기) 기능을 적절히 활용할 것입니다.
결과적으로 행렬을 기약행사다리꼴로 만들고 피벗 성분을 찾을 수 있게 될 것입니다.
반응형