3차원에서 선형 독립
아래와 같이 3차원 공간에서, 3차원 공간을 만들기 위해서는 3개의 벡터가 모두 선형 독립이어야 합니다.

n차원에서 선형 독립
마찬가지로, Rn의 경우
n차원 공간에서 n개의 벡터가 모두 선형독립이어야 합니다.
하나의 벡터를 span하면 선이 됩니다.
즉, R1은 R2를 정의할 수 없습니다.
vector 2개를 span 하면 면(plane)이 됩니다.
R2에서 3개 이상의 벡터가 있다면 그 벡터들의 경우 최소 두 개 이상의 벡터가 선형 의존적 입니다. (Linearly dependent)
즉, Rn에서 필요한 n개 보다 벡터가 적으면 공간을 정의할 수 없고,
n개 보다 많으면 linearly dependent한 벡터가 무조건 존재합니다.
3차원에서 선형 독립 판별
3차원에서 선형 독립에 대한 예시를 들어보겠습니다.
아래와 같이 3개의 벡터가 주어졌다고 하겠습니다.
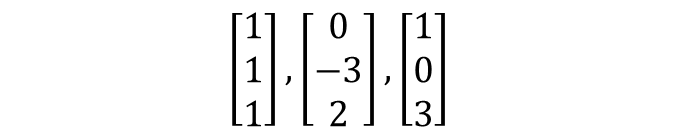
그렇다면, 위 3개의 벡터에서 아래 방정식을 만족하는 해가 몇 개 있을까요??
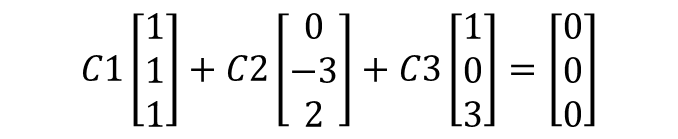
우선, 아래와 같이 나타낼 수 있겠습니다.
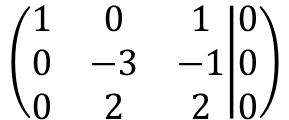
몇 가지 행렬 연산을 수행하면, 아래와 같은 행렬을 만들 수 있게 됩니다.
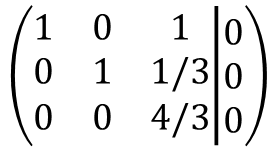
이제 아래 두 연산을 해서 마무리 해보겠습니다.
R1-R3x(3/4) → R1
R2-R3x(1/4) → R2
R3x(3/4) → R3
그러면 아래와 같은 행렬이 완성됩니다.
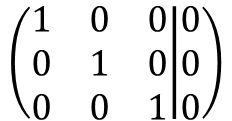
위 행렬은 저희가 이전에 공부했던 기약행사다리꼴(RREF) 입니다!!
기약행사다리꼴의 참고는 아래 링크를 확인해주세요.
[참고. 선형 대수 - 4. 가우스 조던 소거법 (Gauss-Jordan Elimination) (tistory.com)]
이제 첫번째 식을 다시 작성해보도록 하겠습니다.
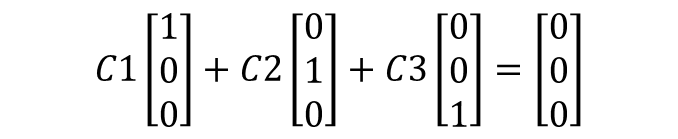
위 식을 만족하는 C1, C2, C3는 C1 = C2 = C3 = 0으로 유일하게 정의됩니다.
즉, 세 벡터는 선형 독립이었고, span하면 3차원 공간을 이루게 됩니다.
이제 벡터, 선형 독립, span의 관계가 어떤것인지 충분히 감을 잡았습니다.
다음 시간에는 선형 부분공간에 대해서 다뤄보도록 하겠습니다. 감사합니다.
'공부 > 선형대수' 카테고리의 다른 글
| FN, FP, TN, TP의 정의와 활용 (Confusion Matrix) (0) | 2025.01.10 |
|---|---|
| 선형 대수 - 11. 선형독립 (2차원) (2) | 2023.10.07 |
| 선형 대수 - 10. 선형 결합 & span (5) | 2023.10.04 |
| 선형 대수 - 9. 유닛 벡터와 기저 벡터 (5) | 2023.10.03 |
| 선형 대수 - 7. 제거 행렬 (Elimination Matrix) (5) | 2023.09.24 |
| 선형 대수 - 6. 행렬의 곱 (42) | 2023.09.14 |
| 선형대수 5. 행렬의 덧셈과 뺄셈 (28) | 2023.09.10 |
| 선형 대수 - 4. 선형계에 대한 해답 (27) | 2023.09.08 |


